Programmation appliquée en Scala

Generic Types and Functions

• Generic type has type parameters. Example: Map[K, V]
• Instantions of type Map[String, Int], Map[Person, Person], ...
• Classes and traits can be generic
• Generic function has type parameters. Example:

  def getMiddle[T](a: Vector[T]) = a(a.length / 2)
  

• Instantiations of function getMiddle[Int], getMiddle[String], ...
• Functions and methods can be generic

Upper Bounds

• Consider Pair type where both components have the same type:

  class Pair[T](val first: T, val second: T)
  

• Add method to produce the smaller value:

  class Pair[T](val first: T, val second: T) {
    def smaller = if (first.compareTo(second) < 0) first else second // Error
  }
  

• That can't work—not every T has a comparable method
• Remedy: Specify an “upper bound”

  class Pair[T <: Comparable[T]]

• T must be a subtype of Comparable[T]

Super- and Subtypes

• In the theory of types, have relationships between types S and T.
• Intuitively, S is a subtype of T, if you can provide a value of type S whenever a type T is expected.
• Notation S <: T
• Example: If the class Student extends Person, then Student <: Person
• Example: Vector[Int] <: Seq[Int]
• If S is a subtype of T, then T is a supertype of S
• Is Int a subtype of Double? Not in Scala—but there is an automatic conversion from Int to Double.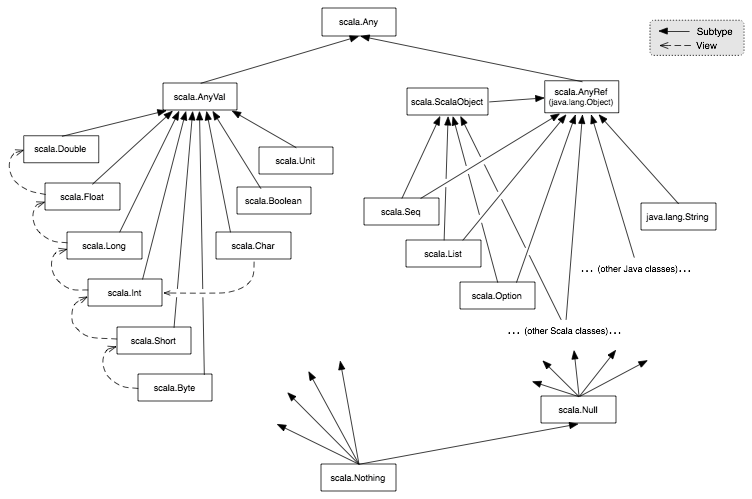

Scala Type Hierarchy

How Many Statements are Correct?

1. Null is a subtype of all Scala types
2. Nothing is a supertype of all Scala types
3. Unit is a subtype of all Scala types
4. An instance of any Scala type can be converted to Unit

1. None of them is correct
2. One is correct of them is correct
3. Two are correct
4. All are correct

Lower Bounds

• Consider Pair class with replaceFirst method:

  class Pair[T](val first: T, val second: T) {
    def replaceFirst(newFirst: T) = new Pair[T](newFirst, second)
  }

  Note that replaceFirst returns a new object—Pair is immutable
• Suppose we have a Pair[Student] and a Person object. Can we call

  students.replaceFirst(person)

• Sure, but the result should be a Pair[Person].
• In general, the replacement type can be a supertype of T.
• Use lower bound:

  def replaceFirst[R >: T](newFirst: R) = new Pair[R](newFirst, second)
  

• Note: The return type can be inferred:

  def replaceFirst[R >: T](newFirst: R) = new Pair(newFirst, second)
  

Context Bounds

• A context bound requires that there is an “implicit value” for a type. For example,

  class Pair[T : Ordering]

  requires an implicit value of type Ordering[T]
• Ordering[T] defines a method compare(T, T)
• Suppose we want a Pair[Int]
• “Somewhere”, there must be a definition

  implicit object NameDoesNotMatter extends Ordering[Int] {
    def compare(a: Int, b: Int) = if (a < b) -1 else if (a > b) 1 else 0
  }

• implicitly fetches implicit object:

  class Pair[T : Ordering](val first: T, val second: T) {
    def smaller =
      if (implicitly[Ordering[T]].compare(first, second) < 0) first else second
  }

Lab

• You work with a buddy
• One of you (the coder) writes the code, the other (the scribe) types up answers
• When you get stuck, ask your buddy first!
• Switch coder/scribe roles each lab
• The coder submits the worksheet. Include the scribe's name in the worksheet!
• The scribe submits answers. Include the coder's name in the report!

Part 1: Upper Bounds

1. Using classes

   class Person(val name: String)
   class Student(name: String, val major: String) extends Person(name)
   

   and the Pair class from the “Lower Bounds” slide

   class Pair[T](val first: T, val second: T) {
     def replaceFirst[R >: T](newFirst: R) = new Pair(newFirst, second)
   }
   

   make a Pair[Student], and then replace the first element with a Person object. What is the type of the result? Why?

2. Now do the opposite, making a Pair[Person], and replacing the first element with a Student object. What is the type of the result? Why?
3. Now remove the upper bound in the replaceFirst method:

   def replaceFirst[R](newFirst: R) = new Pair(newFirst, second)
   

   Note that the method still compiles. Repeat the preceding experiments, replacing the first element in a Pair[Student] and Pair[Person]. Which of them still work? Pay close attention to the types of the returned pairs!

Part 2: Generic Functions

1. Define a generic function swap that swaps the components of a 2-tuple. For example, swap((2, "Hi")) should be ("Hi", 2)
2. Define a generic function sort that sorts the components of a 2-tuple of type (T, T) (where both components have the same type). Require the type to implement the Comparable interface. Hint: Swap them if they are not in order. For example, sort(("Hi", "Bye")) should be ("Bye", "Hi").
3. Define a generic function sort that sorts the components of a 2-tuple of type (T, T), given a comparison function. For example,

   sort(("Hi", "Bye"), (s: String, t: String) => s.length - t.length)

4. What happens when you call

   sort((4, 3), _ - _)

5. Fix that with a curried generic function csort so that csort((4, 3))(_ - _) works.

Part 3: View Bounds

1. What happens when you call the sort method from Part 2 with the pair (4, 3)?
2. The trouble is that Int does not implement Comparable[Int]. It's actually not easy to verify that. But try this:

   val x1 = 3
   x1.getClass
   val x2: Comparable[Int] = 3
   x2.getClass
   

   What are the classes of x1 and x2?
3. Integers are automatically converted to RichInt when needed. In the Scaladoc of RichInt, click on “Linear Supertypes”. Note that Comparable[Int] is a supertype. So, the following should work:

   import scala.runtime.RichInt
   sort((new RichInt(4), new RichInt(3)))

   But it doesn't. Why? (Hint: What is T in this case? What is Comparable[T]? Is T a subtype of Comparable<T>?)
4. This is a common problem, caused by the multitude of automatic conversions that are needed to make Scala work with Java types. The remedy is to use a weaker relationship than subtyping, written as S <% T, to indicate that S can be implicitly converted to a subtype of T. In the definition of sort, change <: to <%. Can you now sort a pair of Int? A pair of RichInt? Explain why.
5. The Comparable interface is used in Java. In Scala, we prefer Ordered. Consider this method:

   def osort[T <: Ordered[T]](pair: (T, T)) =
     if (pair._1 < pair._2) pair else swap(pair)

   What happens if you call osort(("Hi", "Bye"))?
6. Why does that happen? (Hint: Find out what a java.lang.String is automatically converted to when an Ordered[String] is needed.)
7. How do you fix it?

Part 4: Context Bounds

1. The <% trick is a bit icky, and it's no longer recommended. Instead, use a context bound. Complete the following function, using the same logic as in the “Context Bounds” slide.

   def psort[T : Ordering](pair: (T, T)) = ...

2. Verify that psort works for pairs of strings and integers. What did you try?
3. Now add this class to the worksheet:

   class Point(val x: Double, val y: Double) {
     override def toString = s"(${x},${y})"
   }

What happens when you pass two Point objects to psort?
4. Add a definition

   implicit object NameDoesNotMatter extends Ordering[Point] {
       def compare(a: Point, b: Point) = ...
   }

and define comparison of points in some way of your choice. What happens to the call to psort in the preceding step?