Programmation appliquée en Scala

Handling Nested Sequences

We can extend the usage of higher order functions on sequences to many
calculations which are usually expressed using nested loops.

Example: Given a positive integer n, find all pairs of positive integers i and j, with 1 <= j < i < n such that i + j is prime.

For example, if n = 7, the sought pairs are

Algorithm

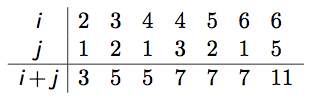
A natural way to do this is to:

• Generate the sequence of all pairs of integers (i, j) such that 1 <= j < i < n.
• Filter the pairs for which i + j is prime.

One natural way to generate the sequence of pairs is to:

• Generate all the integers i between 1 and n (excluded).
• For each integer i, generate the list of pairs (i, 1), ..., (i, i-1).

This can be achieved by combining until and map:

  (1 until n) map (i =>
     (1 until i) map (j => (i, j)))

Question

What is the type of the result?

  (1 until n) map (i =>
     (1 until i) map (j => (i, j)))

Generate Pairs

The previous step gave a sequence of sequences, let's call it xss.

We can combine all the sub-sequences using foldRight with ++:

  (xss foldRight Seq[Int]())(_ ++ _)

Or, equivalently, we use the built-in method flatten

  xss.flatten

This gives:

  ((1 until n) map (i =>
      (1 until i) map (j => (i, j)))).flatten

Generate Pairs (2)

Here's a useful law:

 xs flatMap f  =  (xs map f).flatten

Hence, the above expression can be simplified to

(1 until n) flatMap (i =>
   (1 until i) map (j => (i, j)))

Assembling the pieces

By reassembling the pieces, we obtain the following expression:

(1 until n) flatMap (i =>
   (1 until i) map (j => (i, j))) filter ( pair =>
      isPrime(pair._1 + pair._2))

This works, but makes most people's head hurt.

Is there a simpler way?

For-Expressions

Higher-order functions such as map, flatMap or filter provide powerful constructs for manipulating lists.

But sometimes the level of abstraction required by these function make the program difficult to understand.

In this case, Scala's for expression notation can help.

For-Expression Example

Let persons be a list of elements of class Person, with fields name and age.

  case class Person(name: String, age: Int)

To obtain the names of persons over 20 years old, you can write:

  for ( p <- persons if p.age > 20 ) yield p.name

which is equivalent to:

  persons filter (p => p.age > 20) map (p => p.name)

The for-expression is similar to loops in imperative languages, except
that it builds a list of the results of all iterations.

Syntax of For

A for-expression is of the form

  for ( s ) yield e

where s is a sequence of generators and filters,
and e is an expression whose value is returned by an iteration.

• A generator is of the form p <- e,
  where p is a pattern and e an expression whose value is a collection.
• A filter is of the form if f where f is a boolean expression.
• The sequence must start with a generator.
• If there are several generators in the sequence, the last generators vary faster than the first.

Instead of ( s ), braces { s } can also be used, and then the
sequence of generators and filters can be written on multiple lines
without requiring semicolons.

Use of For

Here are two examples which were previously solved with higher-order functions:

Given a positive integer n, find all the pairs of positive integers
(i, j) such that 1 <= j < i < n, and i + j is prime.

   for {
      i <- 1 until n
      j <- 1 until i
      if isPrime(i + j)
   } yield (i, j)

Exercise

Write a version of scalarProduct (see last session) that makes use of
a for:

  def scalarProduct(xs: List[Double], ys: List[Double]) : Double =

Combinatorial Search Example

In the following we are going to see Sets which are another fundamental collection type.

We then combine Sets and For Expressions in a classical combinatorial search problem, namely the N-Queens problem.

Sets

Sets are another basic abstraction in the Scala collections.

So far, all the collections we have seen were sequences. But there are also two other two other fundamental class of collections: Setsand Maps

A set is written analogously to a sequence:

  val fruit = Set("apple", "banana", "pear")
      //> fruit  : scala.collection.immutable.Set[String] = Set(apple, banana, pear)
  val s = (1 to 6).toSet
      //> s  : scala.collection.immutable.Set[Int] = Set(5, 1, 6, 2, 3, 4)

Most operations on sequences are also available on sets:

  s map (_ + 2)
      //> res1: scala.collection.immutable.Set[Int] = Set(5, 6, 7, 3, 8, 4)
  fruit filter (_.startsWith("app"))              
      //> res2: scala.collection.immutable.Set[String] = Set(apple)
  s.nonEmpty
      //> res3: Boolean = true

(see Iterables Scaladoc for a list of all supported operations)

Sets vs Sequences

The principal differences between sets and sequences are:

$1.$ Sets are unordered; the elements of a set do not have a predefined order in which they appear in the set

$2.$ sets do not have duplicate elements:

  s map (_ / 2)      // Set(2, 0, 3, 1)

$3.$ The fundamental operation on sets is contains:

  s contains 5       // true

Example: N-Queens

The eight queens problem is to place eight queens on a chessboard so that no queen is threatened by another.

In other words, there can’t be two queens in the same row, column, or diagonal.

We now develop a solution for a chessboard of any size, not just 8.

One way to solve the problem is to place a queen on each row.

Once we have placed k - 1 queens, one must place the kth queen in a column where it’s not “in check” with any other queen on the board.

Algorithm

We can solve this problem with a recursive algorithm:

• Suppose that we have already generated all the solutions consisting of placing k-1 queens on a board of size n.
• Each solution is represented by a list (of length k-1) containing the numbers of columns (between 0 and n-1).
• The column number of the queen in the k-1th row comes first in the list, followed by the column number of the queen in row k-2, etc.
• The solution set is thus represented as a set of lists, with one element for each solution.
• Now, to place the kth queen, we generate all possible extensions of each solution preceded by a new queen:

Implementation

  def queens(n: Int) = {
   def placeQueens(k: Int): Set[List[Int]] = {
      if (k == 0) Set(List())
      else
         for {
            queens <- placeQueens(k - 1)
            col <- 0 until n
            if isSafe(col, queens)
         } yield col :: queens
   }
      placeQueens(n)
   }

Exercise

Write a function

   def isSafe(col: Int, queens: List[Int]): Boolean

which tests if a queen placed in an indicated column col is secure amongst the other placed queens.

It is assumed that the new queen is placed in the next availabale row after the other placed queens (in other words: in row queens.length).

Steps:

• We first need to decode the column and row numbers
  => transform the list of column numbers to list of tuples representing row and column numbers
• make sure that for all the queens in the queens list, the new queen given by col is not in check:
• • not in the same column
  • not in diagonal

Queries with for

The for notation is essentially equivalent to the common operations of
query languages for databases.

Example: Suppose that we have a database books, represented as a list of books.

  case class Book(title: String, authors: List[String])

A Mini-Database

  val books: List[Book] = List(
    Book(title   = "Structure and Interpretation of Computer Programs",
	 authors = List("Abelson, Harald", "Sussman, Gerald J.")),
    Book(title   = "Introduction to Functional Programming",
	 authors = List("Bird, Richard", "Wadler, Phil")),
    Book(title   = "Effective Java",
	 authors = List("Bloch, Joshua")),
    Book(title   = "Java Puzzlers",
	 authors = List("Bloch, Joshua", "Gafter, Neal")),
    Book(title   = "Programming in Scala",
	 authors = List("Odersky, Martin", "Spoon, Lex", "Venners, Bill")))

Some Queries

To find the titles of books whose author’s name is “Bird”:

  for (b <- books; a <- b.authors if a startsWith "Bird,")
  yield b.title

To find all the books which have the word “Program” in the title:

  for (b <- books if b.title indexOf "Program" >= 0)
  yield b.title

Another Query

To find the names of all authors who have written at least two books present in the database.

  for {
    b1 <- books
    b2 <- books
    if b1 != b2
    a1 <- b1.authors
    a2 <- b2.authors
    if a1 == a2
  } yield a1

Why do solutions show up twice?

How can we avoid this?

Modified Query

To find the names of all authors who have written at least two books present in the database.

  for {
    b1 <- books
    b2 <- books
    if b1.title < b2.title 
    a1 <- b1.authors
    a2 <- b2.authors
    if a1 == a2
  } yield a1

Problem

What happens if an author has published three books?

1. The author is printed once
2. The author is printed twice
3. The author is printed three times
4. The author is not printed at all

Another possibility is to use the operation withDefaultValue that turns a map into a
total function:

  val cap1 = capitalOfCountry withDefaultValue "<unknown>"
  cap1("Andorra")             // "<unknown>"

You can take look at different operations in class Map here.

Sorted and GroupBy

Two useful operation of SQL queries in addition to for-expressions are
groupBy and orderBy.

orderBy on a collection can be expressed by sortWith and sorted.

  val fruit = List("apple", "pear", "orange", "pineapple")
  fruit sortWith (_.length < _.length)  // List("pear", "apple", "orange", "pineapple")
  fruit.sorted      // List("apple", "orange", "pear", "pineapple")

groupBy is available on Scala collections. It partitions a collection
into a map of collections according to a discriminator function f.

Example:

  fruit groupBy (_.head)  //> Map(p -> List(pear, pineapple),
			  //|     a -> List(apple),
			  //|     o -> List(orange))

Map Example

A polynomial can be seen as a map from exponents to coefficients.

For instance, $x^3 - 2x + 5$ can be represented with the map.

  Map(0 -> 5, 1 -> -2, 3 -> 1)

Based on this observation, let’s design a class Polynom that represents polynomials as maps.

Implementation of Polynom

class Poly(val terms0: Map[Int, Double]) {
  val terms = terms0 withDefaultValue 0.0
  
  def + (other: Poly) : Poly = {
    val newKeySet = terms.keySet ++ other.terms.keySet
	val setOfTuples = for(x <- newKeySet) yield
      ( x -> (terms(x) + other.terms(x)))
	new Poly(setOfTuples.toMap)
  } 
}

Variable Length Argument Lists

It’s quite inconvenient to have to write

  Polynom(Map(1 -> 2.0, 3 -> 4.0, 5 -> 6.2))

Can one do without the Map(...)?

Problem: The number of key -> value pairs passed to Map can vary.

We can accommodate this pattern using a repeated parameter:

   def Polynom(bindings: (Int, Double)*) =
     new Polynom(bindings.toMap withDefaultValue 0)
   
   Polynom(1 -> 2.0, 3 -> 4.0, 5 -> 6.2)

Inside the Polynom function, bindings is seen as a
Seq[(Int, Double)].

Final Implementation of Polynom

class Poly(val terms0: Map[Int, Double]) {
  def this(bindings: (Int, Double)*) = this(bindings.toMap)
  val terms = terms0 withDefaultValue 0.0
  
  def + (other: Poly) : Poly = {
    val newKeySet = terms.keySet ++ other.terms.keySet
	val setOfTuples = for(x <- newKeySet) yield
      ( x -> (terms(x) + other.terms(x)))
	new Poly(setOfTuples.toMap)
  } 
  override def toString =
  (for ((exp, coeff) <- terms.toList.sorted.reverse)
    yield coeff+"x^"+exp) mkString " + "
}

Last exercice for this unit!

Using for expressions write a function to find the numbers x,y,z below n such that $x^2 + y^2 == z^2$

Homework

Do this as individual work, not with your partner

When all done, email the signed zip files to Fatemeh.Borran@heig-vd.ch

• Problem 1
• Problem 2
• Problem 3
• Problem 4
• Problem 5
• Problem 6