Programmation appliquée en Scala

Context-Free Grammar

• Language: Set of valid token sequences
• Terminal symbol: Token in the language. Ex: "class" "3.14" "("
• Nonterminal symbol: Symbols in the grammar. Ex. term
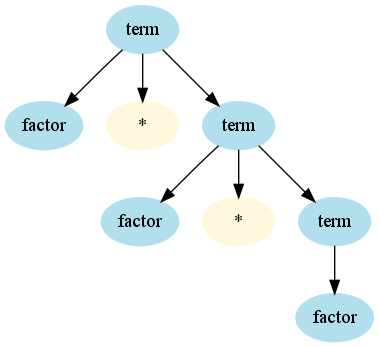
• Production: Rule for replacing a nonterminal by a sequence of nonterminals and terminals

  term ::= factor * term

• Can have more than one production for the same nonterminal

  term ::= factor

• Derivation: Sequence of productions

  term ::= factor * term
    ::= factor * factor * term
    ::= factor * factor * factor

• Context-free: The replacement doesn't depend on the context of the nonterminal

Parse Tree

• Shows derivation process

  

• Not the same as an expression tree!
• Parser: Component that follows derivation process, yielding some actions
• Most common action: Building an expression tree.

Combinator Parser

• Each nonterminal becomes a function
• Terminals (strings) and nonterminals (functions) are combined with operators
  • Sequence ~
  • Alternative |
  • 0 or more rep(...)
  • 0 or 1 opt(...)

  class SimpleLanguageParser extends JavaTokenParsers {    
    def expr: Parser[Any] = term ~ opt(("+" | "-") ~ expr)
    def term: Parser[Any] = factor ~ opt(("*" | "/" ) ~ term)
    def factor: Parser[Any] = wholeNumber | "(" ~ expr ~ ")"
  }

• Will replace Parser[Any] with something more useful later

Combinator Parser Result

• String returns itself
• opt(P) returns Option: Some of the result of P, or None
• rep(P) returns List of the results of P
• P ~ Q returns instance of class ~ (similar to a pair)
• For example,

  val parser = new SimpleLanguageParser
  val result = parser.parse(parser.expr, "3 - 4 * 5")

  sets result to

  ((3~None)~Some((-~((4~Some((*~(5~None))))~None))))

• We'll transform this to something more useful in the next slide

Transforming Combinator Parser Results

• Use ^^ operator to transform. For example,

  wholeNumber ^^ (_.toDouble) 

• Use pattern matching for transforms

  def expr: Parser[Double] = (term ~ opt(("+" | "-") ~ expr)) ^^ { 
    case a ~ None => a
    case a ~ Some("+" ~ b) => a + b
    case a ~ Some("-" ~ b) => a - b
    }

• Use ~>, <~ to discard tokens

  def factor: Parser[Double] = wholeNumber ^^ (_.toDouble) |
     "(" ~> expr <~ ")"

• The Parser[...] type must match the return type of the transforms (here, Double)

Returning Expression Trees

• Returning Double works if we interpret an arithmetic expression without variables
• For interpreters, code generators, want an expression tree: Parser[Expr]

  class Expr
  case class Number(value : Int) extends Expr
  case class Variable(name : String) extends Expr
  case class Sum(left : Expr, right : Expr) extends Expr

• class SimpleLanguageParser extends JavaTokenParsers {    
    def expr: Parser[Expr] = (term ~ opt(("+" | "-") ~ expr)) ^^ { 
      case a ~ None => a
      case a ~ Some("+" ~ b) => Sum(a, b)
      case a ~ Some("-" ~ b) => Difference(a, b)
    } 
    ...
  }

• Returns tree such as

  Difference(Number(3),Product(Number(4),Number(5)))

A Grammar Problem

• Consider the input 3 - 4 - 5
• Parse:

  expr ::= term - expr
    ::= term - term - expr
    

• Resulting expression tree:

  

• That's the wrong tree. 3 - (4 - 5) is 3 - (-1) = 4
• We want - to be left associative: (3 - 4) - 5
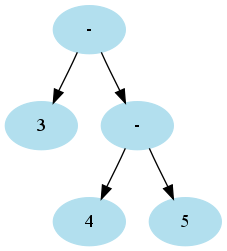
• How about switching expr and term?
• In theory, this works, but in practice, the Scala combinator parser gets into an infinite recursion

  expr ::= expr - term 
   ::= expr - expr - term
   :: expr - expr - expr - term

Remedy: Manually Group Terms

• Reorganize Grammar

  class SimpleLanguageParser extends JavaTokenParsers {    
    def expr: Parser[Expr] = term ~ rep(("+" | "-") ~ term)
    def term: Parser[Expr] = factor ~ rep(("*" | "/" ) ~ factor)
    def factor: Parser[Expr] = wholeNumber | "(" ~ expr ~ ")"
  }

• Now we have a list of all terms
• Manually group them left to right

  Operator(Operator(...(Operator(term1, term2), term3)), ...)

• Use foldLeft—see next slide

Use foldLeft

• Parsing 3 - 4 - 5 yields

  3 ~ List("-" ~ 4, "-" ~ 5)

• Note that the tail is a flat list
• Want the tree

      -
     / \
    -   5
   / \
  3   4

• Initial element is 3
• Next element is "-" ~ 4
• Fold operator is

  case (x, "+" ~ y) => Sum(x, y)
  case (x, "-" ~ y) => Difference(x, y)

• Now everything together:

  def expr: Parser[Expr] = (term ~ rep(("+" | "-") ~ term)) ^^ { 
      case a ~ lst =>  lst.foldLeft(a) { 
        case (x, "+" ~ y) => Sum(x, y)
        case (x, "-" ~ y) => Difference(x, y)
      }

• Result: Parser yields Expr with the correct structure

Repetition

• Simple repetition, ex. array bounds [10][10][20]
• Use rep convenience combinator

  def bounds = rep(bound)
  bound = "[" ~> wholeNumber <~ "]" ^^ { _.toInt } 

• Repetition with separators, ex. function arguments id(arg1, arg2, ...)
• Use repsep convenience combinator

  def funcall = ident ~ "(" ~> repsep(expr, ",") <~ ")"

  repsep returns List without separators; here, List[Expr]

Lab

• You work with a buddy
• One of you (the coder) writes the code, the other (the scribe) types up answers
• When you get stuck, ask your buddy first!
• Switch coder/scribe roles each lab
• The coder submits the worksheet. Include the scribe's name in the worksheet!
• The scribe submits answers. Include the coder's name in the report!

Part 1: Expressions

1. Make a new project unit12. Right-click on the project in the tree display at the left, select Properties → Java Build Path → Libraries → Add External JARs, then locate to the directory where the Scala IDE is installed, go to its plugins directory, and pick org.scala-lang.modules.scala-parser-combinators_1.0.1.jar.
2. Then restart the Scala IDE.
3. Make a worksheet expr.sc. Paste in this code:

   import scala.util.parsing.combinator._
   class ExprParser extends JavaTokenParsers {
   	def expr: Parser[Any] = term ~ rep(("+" | "-") ~ term)
   	def term: Parser[Any] = factor ~ rep("*" ~> factor)
   	def factor: Parser[Any] = wholeNumber | "(" ~ expr ~ ")"
   }
   
   val parser = new ExprParser
   parser.parseAll(parser.expr, "3-4*5")

   What do you get?
4. That's not so instructive. Make a copy of the ExprParser class and call it ExprParser2. Change all the Parser[Any] to Parser[Int]. Now you need to put ^^ transforms behind each result. I'll give you two of them:

   ... (term ~ rep(("+" | "-") ~ term)) ^^ { 
       case a ~ lst =>  (lst.foldLeft(a)) {
         	case (x, "+" ~ y) => x + y
         	case (x, "-" ~ y) => x - y
       }
   
   ... wholeNumber ^^ { _.toInt }
   

   Figure out the other two.
5. Now call

   val parser2 = new ExprParser2
   parser2.parseAll(parser2.expr, "3-4*5")

   What happens?
6. That's nice. Now we have a calculator. But what if we want to build a compiler? Then we need a parse tree. First define

   class Expr
   case class Number(value : Int) extends Expr
   case class Sum(left : Expr, right : Expr) extends Expr
   case class Difference(left : Expr, right : Expr) extends Expr
   case class Product(left : Expr, right : Expr) extends Expr
   

   Now we want to make a Parser[Expr], not a Parser[Int]. So, change all the return types and change the ^^ expressions to yield instances of Expr subclasses. I'll give you one:

   ...factor ~ rep("*" ~> factor) ^^ {
     case f ~ r => r.foldLeft(f)(Product(_, _))
   }
   

7. Now what do you get for

   val parser3 = new ExprParser3
   arser3.parseAll(parser3.expr, "3-4*5")

Part 2: JSON Parsing

1. You have probably seen JSON, the JavaScript object notation. It is ubiquitous in web programming. It lets you describe arrays and maps of key/value pairs, where the keys are strings. Here is an example:

   [{"balance" : 10000}, "Harry", true]
   

   Check out the JSON web site. It uses “railroad diagrams” to show the JSON syntax. It's trivial to turn them into a parser:

   class JSONParser extends JavaTokenParsers {
       def value: Parser[Any] = stringLiteral | floatingPointNumber | obj | array | "true" | "false" | "null"
       def member: Parser[Any] = stringLiteral ~ ":" ~ value
       def obj: Parser[Any] = "{" ~ repsep(member, ",") ~ "}"
       def array: ...
     }

   Here, stringLiteral and floatingPointNumber are defined in the JavaTokenParsers to parse, you guessed it, a string literal and a floating point number.
   I left it for you to fill in the entry for array.
2. Make a JSONParser and parse """[{"balance" : 10000}, "Harry", true]""". The """...""" is a convenient Scala syntax for string literals that can contain ", so you don't have to write "[{\"balance\" : 10000}, \"Harry\", true]" What do you get?
3. Ok, that's no good. In a Scala program, we want to use the JSON expression. We could either turn it into nested case class instances, like in the preceding exercise, or, more brutally, make an object into a Map[String, Any] and an array into a List[Any]. That's what we'll do now.
   Copy the JSONParser class into JSONParser2. A value is still an Any, but a member is a pair (String, Any), an obj is a Map[String, Any], and an array is a List[Any]. Update the Parser type parameters.
4. Next, add ^^ { ... } clauses. I'll just give you the ones for false, true, and null:

   ... "true" ^^ { _ => true } | "false" ^^ { _ => false } | "null" ^^ { _ => null }

   For a member, you want to get a pair. Do this so that you don't get error messages.
5. For an obj, use ~> and <~ to get rid of the { } delimiters. Then the result is a list of members, i.e. a list of pairs. Call _.toMap to turn it into a map.
6. Finally, use ~> and <~ to get rid of the [ ] delimiters for arrays. Then you get a list, and you want a list, so you don't have to do anything.
   Now make a JSONParser2 and parse again """[{"balance" : 10000}, "Harry", true]""" . What do you get?
7. Isn't this amazing? You have parsed JSON, with your bare hands, in less than ten lines of code. Of course, for JSON, you can get an off-the-shelf library, but if you have to parse something less common, such as Dot or asciimath, Scala has you covered.

Homework

Do this as individual work, not with your partner

When all done, email the signed zip files to Fatemeh.Borran@heig-vd.ch

• Problem 1
• Problem 2
• Problem 3
• Problem 4
• Problem 5